Rise and Run

Vandelay Industries doesn’t architect per se. However, when I’m architecting a roof for my potato loving friends in Idaho, I use a few basic math skills. I got to thinking, I should share a few ideas with Seinfelders and future architects. Here are a few tips if you want to pretend to be an architect.

In algebra there is a simple formula for calculating angles of triangles. I utilize this formula almost every day when designing roof trusses. Most all kids in the United States learn this at some point and is usually GED (general equivalency diploma) level of education. In this case today, I want to know how much to chop off the end for a 1/4″ (4/16″) rise for my but cut.

The math

Do not confuse slope with pitch, they are similar in what they do, but are calculated differently. Pitch compares the roof’s span to the rise while slope compares rise and run. Slope can be visualized as a grid of 7 up and 12 over and a linear line from 0,0 -> 7,12. This is also a precursor to vectoring.

I know my rise is 1/4″ or 4/16″. I also know the slope of my roof truss is 7″ over 12′ (or 7″ per foot). If you have two of the three triangle numbers, you can always find the third factor of the equation. We have have Y and Z and we need to solve for X.

Rise / Run = slope

is also

Rise / slope = Run

A rise of 4/16″ divided by a 7/12 slope = 7/16″ run length

I needed to cut 7/16″ off the end of the little corner to have a 1/4″ but cut height.

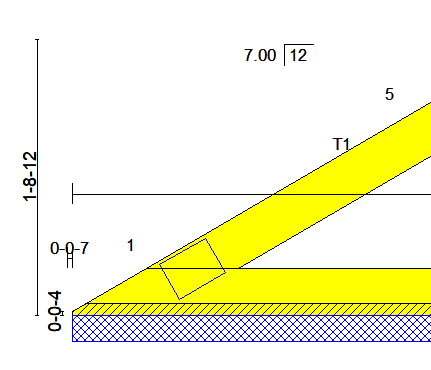
This example is slightly obfuscated by the fact I’m changing my scale of base 16 scale inches and base 12 feet. But the idea remains the same. Try it with whole numbers if you get confused.

Here are a few additional educational resources:

Here is an educational view of how to calculate rise/run/slope from the Khan Academy. Very fun website if you like to learn math.

Click here for a more information from a practical application writeup.